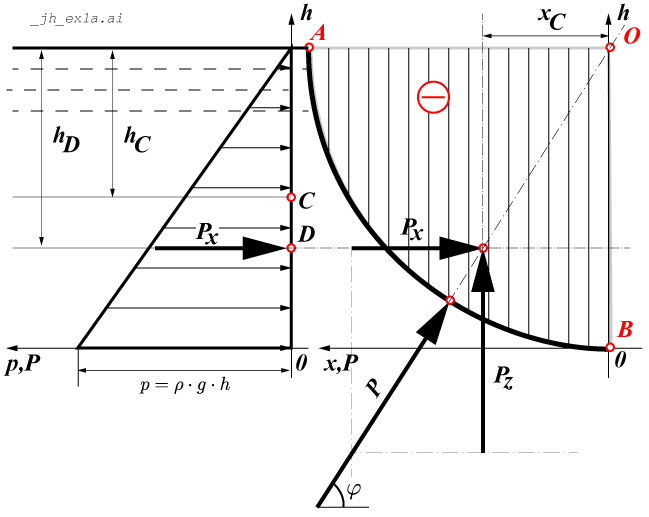
\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)
Conversion Factors

| (%i1) | kill ( all ) ; |
\[\operatorname{ }\ensuremath{\mathrm{done}}\]
| (%i5) | R : 1 ; B : 2 ; ro : 1000 ; g : 9 . 81 ; H : R ; |
\[\operatorname{ }1\]
\[\operatorname{ }2\]
\[\operatorname{ }1000\]
\[\operatorname{ }9.81\]
\[\operatorname{ }1\]
| (%i6) | P_x : integrate ( ro · g · ( H − h ) · B , h , 0 , R ) ; |
\[\]\[rat: replaced 9810.0 by 9810/1 = 9810.0\]
\[\operatorname{ }9810\]
| (%i8) | W_z : integrate ( ( sqrt ( R · · 2 − ( R − h ) · · 2 ) ) · B , h , 0 , R ) $ W_z , numer ; |
\[\operatorname{ }1.5707963267948966\]
| (%i9) | W : ( ( %pi · ( R · · 2 ) ) / 4 ) · B , numer ; |
\[\operatorname{ }1.5707963267948966\]
| (%i10) | P_z : W_z · ro · g , numer ; |
\[\operatorname{ }15409.511965857935\]
| (%i12) | phi_rad : atan ( P_z / P_x ) , numer ; phi_g : ( 180 / %pi ) · phi_rad , numer ; |
\[\operatorname{ }1.0038848218538872\]
\[\operatorname{ }57.51836340947025\]
| (%i13) | w : integrate ( ( sqrt ( R · · 2 − ( R − h ) · · 2 ) ) · B , h , 0 , R ) ; |
\[\operatorname{ }\frac{\ensuremath{\pi} }{2}\]
| (%i14) | mw : integrate ( ( sqrt ( R · · 2 − ( R − h ) · · 2 ) ) · B · ( ( sqrt ( R · · 2 − ( R − h ) · · 2 ) ) / 2 ) , h , 0 , R ) ; |
\[\operatorname{ }\frac{2}{3}\]
| (%i15) | x_C : mw / w , numer ; |
\[\operatorname{ }0.42441318157838753\]
Numerical methods, K123 (Чисельні методи, K123)
| (%i16) | kill ( all ) ; |
\[\operatorname{ }\ensuremath{\mathrm{done}}\]
| (%i5) | R : 1 ; B : 2 ; ro : 1000 ; g : 9 . 81 ; H : R ; |
\[\operatorname{ }1\]
\[\operatorname{ }2\]
\[\operatorname{ }1000\]
\[\operatorname{ }9.81\]
\[\operatorname{ }1\]
P_x
| (%i6) | dh : R / 10000 ; |
\[\operatorname{ }\frac{1}{10000}\]
| (%i8) | h : 0 ; P_x : 0 ; |
\[\operatorname{ }0\]
\[\operatorname{ }0\]
| (%i10) | for i : 1 while h < = R do ( Pi : ro · g · ( H − h ) · B · dh , P_x : P_x + Pi , h : h + dh ) ; P_x ; |
\[\operatorname{ }\ensuremath{\mathrm{done}}\]
\[\operatorname{ }9810.980999999996\]
| (%i12) | h : 0 ; mP_x : 0 ; |
\[\operatorname{ }0\]
\[\operatorname{ }0\]
| (%i14) | for i : 1 while h < = R do ( mPi : ro · g · ( ( H − h ) · · 2 ) · B · dh , mP_x : mP_x + mPi , h : h + dh ) ; mP_x ; |
\[\operatorname{ }\ensuremath{\mathrm{done}}\]
\[\operatorname{ }6540.981032700002\]
| (%i16) | h : 0 ; mP_x_down : 0 ; |
\[\operatorname{ }0\]
\[\operatorname{ }0\]
| (%i18) | for i : 1 while h < = R do ( mPi : ro · g · ( H − h ) · h · B · dh , mP_x_down : mP_x_down + mPi , h : h + dh ) ; mP_x_down ; |
\[\operatorname{ }\ensuremath{\mathrm{done}}\]
\[\operatorname{ }3269.9999672999975\]
| (%i19) | h_D : mP_x / P_x ; |
\[\operatorname{ }0.6667000000000005\]
| (%i20) | h_D_down : mP_x_down / P_x ; |
\[\operatorname{ }0.3332999999999999\]
| (%i21) | h_D + h_D_down ; |
\[\operatorname{ }1.0000000000000004\]
P_z
| (%i26) | R : 1 ; B : 2 ; ro : 1000 ; g : 9 . 81 ; H : R ; |
\[\operatorname{ }1\]
\[\operatorname{ }2\]
\[\operatorname{ }1000\]
\[\operatorname{ }9.81\]
\[\operatorname{ }1\]
| (%i28) | n : 10000 ; dh : R / n ; |
\[\operatorname{ }10000\]
\[\operatorname{ }\frac{1}{10000}\]
| (%i30) | h : 0 ; P_z : 0 ; |
\[\operatorname{ }0\]
\[\operatorname{ }0\]
| (%i33) | fB ( h ) : = ( sqrt ( R · · 2 − ( R − h ) · · 2 ) ) ; fB ( 0 ) ; fB ( R ) ; |
\[\operatorname{ }\operatorname{fB}(h)\operatorname{:=}\sqrt{{{R}^{2}}\operatorname{-}{{\left( R\operatorname{-}h\right) }^{2}}}\]
\[\operatorname{ }0\]
\[\operatorname{ }1\]
| (%i34) | fb : fB ( h ) ; |
\[\operatorname{ }0\]
| (%i36) | for i : 1 thru n step 1 do ( fb1 : fB ( h ) , dfb : fb1 − fb , Pi : ro · g · ( H − h ) · dfb · B , P_z : P_z + Pi , h : h + dh , fb : fb1 ) ; Pz : P_z , numer ; |
\[\operatorname{ }\ensuremath{\mathrm{done}}\]
\[\operatorname{ }15408.52519768357\]
| (%i38) | h : 0 ; mP_z : 0 ; |
\[\operatorname{ }0\]
\[\operatorname{ }0\]
| (%i39) | fb : fB ( h ) ; |
\[\operatorname{ }0\]
| (%i41) | for i : 1 thru n step 1 do ( fb1 : fB ( h ) , dfb : fb1 − fb , mPi : ro · g · ( H − h ) · dfb · B · fB ( h ) , mP_z : mP_z + mPi , h : h + dh , fb : fb1 ) ; mPz : mP_z , numer ; |
\[\operatorname{ }\ensuremath{\mathrm{done}}\]
\[\operatorname{ }6545.153696629369\]
| (%i42) | x_D : mPz / Pz ; |
\[\operatorname{ }0.4247748316375749\]
Analytical calculations using the three-team method K123
| (%i43) | kill ( all ) ; |
\[\operatorname{ }\ensuremath{\mathrm{done}}\]
| (%i5) | R : 1 ; B : 2 ; ro : 1000 ; g : 9 . 81 ; H : R ; |
\[\operatorname{ }1\]
\[\operatorname{ }2\]
\[\operatorname{ }1000\]
\[\operatorname{ }9.81\]
\[\operatorname{ }1\]
P_x
| (%i6) | P : integrate ( rho · gi · ( Hi − h ) · Bi , h ) ; |
\[\operatorname{ }\ensuremath{\mathrm{Bi}}\, \ensuremath{\mathrm{gi}}\, \left( \ensuremath{\mathrm{Hi}} h\operatorname{-}\frac{{{h}^{2}}}{2}\right) rho\]
| (%i7) | fP ( h ) : = B · g · ( R · h − ( ( h · · 2 ) / 2 ) ) · ro ; |
\[\operatorname{ }\operatorname{fP}(h)\operatorname{:=}B g\, \left( R h\operatorname{-}\frac{{{h}^{2}}}{2}\right) \, \ensuremath{\mathrm{ro}}\]
| (%i8) | fP_x ( B , g , R , ro , h ) : = B · g · ( R · h − ( ( h · · 2 ) / 2 ) ) · ro ; |
\[\operatorname{ }\operatorname{fP\_ x}\left( B\operatorname{,}g\operatorname{,}R\operatorname{,}\ensuremath{\mathrm{ro}}\operatorname{,}h\right) \operatorname{:=}B g\, \left( R h\operatorname{-}\frac{{{h}^{2}}}{2}\right) \, \ensuremath{\mathrm{ro}}\]
| (%i9) | fP_x ( 2 , 9 . 81 , 1 , 1000 , 1 ) ; |
\[\operatorname{ }9810.0\]
| (%i10) | plot2d ( fP_x ( 2 , 9 . 81 , 1 , 1000 , h ) , [ h , 0 , R ] ) ; |
\[\operatorname{ }false\]
| (%i11) | mP : integrate ( rho · gi · ( ( Hi − h ) · · 2 ) · Bi , h ) ; |
\[\operatorname{ }\ensuremath{\mathrm{Bi}}\, \ensuremath{\mathrm{gi}}\, \left( \frac{{{h}^{3}}}{3}\operatorname{-}\ensuremath{\mathrm{Hi}} {{h}^{2}}\operatorname{+}{{\ensuremath{\mathrm{Hi}}}^{2}} h\right) rho\]
| (%i12) | mP_d : integrate ( rho · gi · ( Hi − h ) · Bi · h , h ) ; |
\[\operatorname{ }\operatorname{-}\left( \frac{\ensuremath{\mathrm{Bi}}\, \ensuremath{\mathrm{gi}}\, \left( 2 {{h}^{3}}\operatorname{-}3 \ensuremath{\mathrm{Hi}} {{h}^{2}}\right) rho}{6}\right) \]
| (%i13) | fmP_x ( B , g , H , ro , h ) : = B · g · ( h ^ 3 / 3 − H · h ^ 2 + H ^ 2 · h ) · ro ; |
\[\operatorname{ }\operatorname{fmP\_ x}\left( B\operatorname{,}g\operatorname{,}H\operatorname{,}\ensuremath{\mathrm{ro}}\operatorname{,}h\right) \operatorname{:=}B g\, \left( \frac{{{h}^{3}}}{3}\operatorname{-}H {{h}^{2}}\operatorname{+}{{H}^{2}} h\right) \, \ensuremath{\mathrm{ro}}\]
| (%i14) | plot2d ( fmP_x ( 2 , 9 . 81 , 1 , 1000 , h ) , [ h , 0 , R ] ) ; |
\[\operatorname{ }false\]
| (%i15) | fmP_x ( 2 , 9 . 81 , 1 , 1000 , 1 ) ; |
\[\operatorname{ }6540.0\]
| (%i16) | fh_D : ( fmP_x ( 2 , 9 . 81 , 1 , 1000 , 1 ) ) / ( fP_x ( 2 , 9 . 81 , 1 , 1000 , 1 ) ) ; |
\[\operatorname{ }0.6666666666666666\]
| (%i17) | plot2d ( [ fP_x ( 2 , 9 . 81 , 1 , 1000 , h ) , fmP_x ( 2 , 9 . 81 , 1 , 1000 , h ) ] , [ h , 0 , R ] ) ; |
\[\operatorname{ }false\]
| (%i18) | plot2d ( [ fmP_x ( 2 , 9 . 81 , 1 , 1000 , h ) / fP_x ( 2 , 9 . 81 , 1 , 1000 , h ) ] , [ h , 0 , R ] ) ; |
\[\]\[expt: undefined: 0 to a negative exponent. \]\[plot2d: expression evaluates to non-numeric value somewhere in plotting range.\]
\[\operatorname{ }false\]
P_z
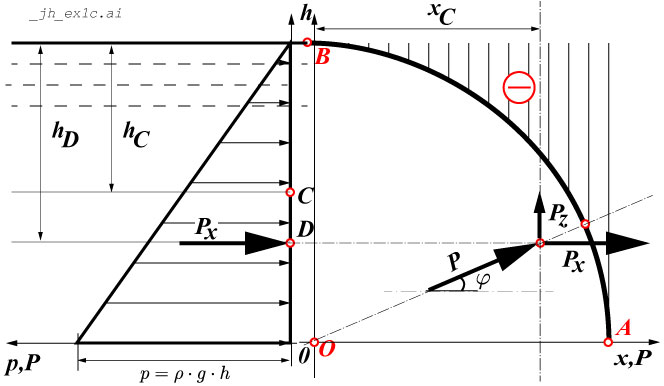
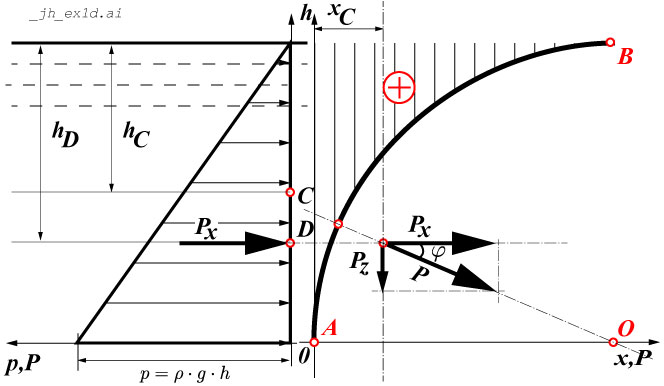
| (%i19) | kill ( all ) ; |
\[\operatorname{ }\ensuremath{\mathrm{done}}\]
| (%i5) | R : 1 ; B : 2 ; ro : 1000 ; g : 9 . 81 ; H : R ; |
\[\operatorname{ }1\]
\[\operatorname{ }2\]
\[\operatorname{ }1000\]
\[\operatorname{ }9.81\]
\[\operatorname{ }1\]
| (%i7) | P_x : integrate ( ro · g · ( H − h ) · B , h , 0 , R ) ; P_x / 9 ; |
\[\]\[rat: replaced 9810.0 by 9810/1 = 9810.0\]
\[\operatorname{ }9810\]
\[\operatorname{ }1090\]
| (%i10) | fB ( h ) : = R − sqrt ( R · · 2 − h · · 2 ) ; fB ( 0 ) ; fB ( R ) ; |
\[\operatorname{ }\operatorname{fB}(h)\operatorname{:=}R\operatorname{-}\sqrt{{{R}^{2}}\operatorname{-}{{h}^{2}}}\]
\[\operatorname{ }0\]
\[\operatorname{ }1\]
| (%i11) | P_z : integrate ( fB ( h ) · B · ro · g , h , 0 , R ) , numer ; |
\[\]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 1.0 by 1/1 = 1.0 \]\[rat: replaced 1.5 by 3/2 = 1.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 1.5 by 3/2 = 1.5 \]\[rat: replaced 2.0 by 2/1 = 2.0 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 1.5 by 3/2 = 1.5 \]\[rat: replaced 2.0 by 2/1 = 2.0 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.21460183660255128 by 5844813/27235615 = 0.21460183660255147\]
\[\operatorname{ }4210.48803414206\]
| (%i12) | mP_z : integrate ( fB ( h ) · B · ro · g · ( R − fB ( h ) / 2 ) , h , 0 , R ) , numer ; |
\[\]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced -0.5 by -1/2 = -0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced -0.5 by -1/2 = -0.5 \]\[rat: replaced 0.16666666666666666 by 1/6 = 0.16666666666666666 \]\[rat: replaced 0.16666666666666666 by 1/6 = 0.16666666666666666\]
\[\operatorname{ }3270.0\]
| (%i16) | x_C : mP_z / P_z ; x_C_ : R − x_C ; 295 · 0 . 22336793894575135 ; 295 · 0 . 7766320610542486 ; |
\[\operatorname{ }0.7766320610542486\]
\[\operatorname{ }0.22336793894575135\]
\[\operatorname{ }65.89354198899665\]
\[\operatorname{ }229.10645801100335\]
| (%i18) | W_test : integrate ( fB ( h ) · B , h , 0 , R ) , numer ; P_z_test : W_test · ro · g ; |
\[\]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 1.0 by 1/1 = 1.0 \]\[rat: replaced 1.5 by 3/2 = 1.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 1.5 by 3/2 = 1.5 \]\[rat: replaced 2.0 by 2/1 = 2.0 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 1.5 by 3/2 = 1.5 \]\[rat: replaced 2.0 by 2/1 = 2.0 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.21460183660255128 by 5844813/27235615 = 0.21460183660255147\]
\[\operatorname{ }0.42920367320510294\]
\[\operatorname{ }4210.488034142059\]
| (%i19) | W_test : ( R · · 2 − ( ( %pi · ( R · · 2 ) ) / 4 ) ) · B , numer ; |
\[\operatorname{ }0.42920367320510344\]
| (%i21) | P_z_test : W_test · ro · g ; P_z_test / 9 ; |
\[\operatorname{ }4210.488034142065\]
\[\operatorname{ }467.83200379356276\]
| (%i23) | P : sqrt ( P_x · · 2 + P_z · · 2 ) ; P / 9 ; |
\[\operatorname{ }10675.406759728337\]
\[\operatorname{ }1186.156306636482\]
| (%i25) | phi_rad : atan ( P_z / P_x ) , numer ; phi_g : ( 180 / %pi ) · phi_rad , numer ; |
\[\operatorname{ }0.40542580169731124\]
\[\operatorname{ }23.229187342963783\]
| (%i26) | kill ( all ) ; |
\[\operatorname{ }\ensuremath{\mathrm{done}}\]
| (%i1) | S : 300 ; |
\[\operatorname{ }300\]
| (%i6) | R : 1 ; B : 2 ; ro : 1000 ; g : 9 . 81 ; H : R / 2 , numer ; |
\[\operatorname{ }1\]
\[\operatorname{ }2\]
\[\operatorname{ }1000\]
\[\operatorname{ }9.81\]
\[\operatorname{ }0.5\]
| (%i7) | P_x : integrate ( ro · g · ( R − h ) · B , h , 0 , H ) ; |
\[\]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.375 by 3/8 = 0.375\]
\[\operatorname{ }7357.5\]
| (%i8) | mP_x : integrate ( ro · g · ( R − h ) · B · ( R − h ) , h , 0 , H ) ; |
\[\]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.2916666666666667 by 7/24 = 0.2916666666666667\]
\[\operatorname{ }5722.5\]
| (%i11) | h_D : mP_x / P_x ; ( R − h_D ) ; ( R − h_D ) · S ; |
\[\operatorname{ }0.7777777777777778\]
\[\operatorname{ }0.2222222222222222\]
\[\operatorname{ }66.66666666666666\]
| (%i12) | fB ( h ) : = sqrt ( R · · 2 − ( R − h ) · · 2 ) ; |
\[\operatorname{ }\operatorname{fB}(h)\operatorname{:=}\sqrt{{{R}^{2}}\operatorname{-}{{\left( R\operatorname{-}h\right) }^{2}}}\]
| (%i13) | P_z : integrate ( ro · g · ( R − h ) · ( fB ( h ) ) · B , h , 0 , H ) , numer ; |
\[\]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 1.5 by 3/2 = 1.5 \]\[rat: replaced 0.3333333333333333 by 1/3 = 0.3333333333333333 \]\[rat: replaced 1.5 by 3/2 = 1.5 \]\[rat: replaced 1.5 by 3/2 = 1.5 \]\[rat: replaced 1.5 by 3/2 = 1.5 \]\[rat: replaced 0.0 by 0/1 = 0.0 \]\[rat: replaced 0.21650635094610962 by 7602076/35112485 = 0.21650635094610934\]
\[\operatorname{ }4247.854605562666\]
| (%i14) | P : sqrt ( P_x · · 2 + P_z · · 2 ) ; |
\[\operatorname{ }8495.70921112534\]
| (%i16) | phi_rad : atan ( P_z / P_x ) , numer ; phi_g : ( 180 / %pi ) · phi_rad , numer ; |
\[\operatorname{ }0.5235987755982983\]
\[\operatorname{ }29.999999999999964\]
| (%i17) | P_z : integrate ( fB ( h ) · B · ro · g , h , 0 , H ) , numer ; |
\[\]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced -0.5 by -1/2 = -0.5 \]\[rat: replaced -0.5 by -1/2 = -0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced -0.5 by -1/2 = -0.5 \]\[rat: replaced -0.5 by -1/2 = -0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced -0.5 by -1/2 = -0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 1.0 by 1/1 = 1.0 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced -0.25 by -1/4 = -0.25 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced -0.125 by -1/8 = -0.125 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 1.0 by 1/1 = 1.0 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.25 by 1/4 = 0.25 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5\]
\[\operatorname{ }19620.0 \left( 0.25 \ensuremath{\pi} \operatorname{-}0.4783057387452591\right) \]
| (%i18) | mP_z : integrate ( fB ( h ) · B · ro · g · ( fB ( h ) / 2 ) , h , 0 , H ) , numer ; |
\[\]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 0.5 by 1/2 = 0.5 \]\[rat: replaced 1.0 by 1/1 = 1.0 \]\[rat: replaced -0.3333333333333333 by -1/3 = -0.3333333333333333 \]\[rat: replaced 0.20833333333333334 by 5/24 = 0.20833333333333334\]
\[\operatorname{ }2043.75\]
| (%i20) | x_C : mP_z / P_z , numer ; S · x_C ; |
\[\operatorname{ }0.3392029835468756\]
\[\operatorname{ }101.76089506406268\]
| --> |
| (%i23) | x : 600 ; y : 150 ; x2 : x / 2 ; |
\[\operatorname{ }600\]
\[\operatorname{ }150\]
\[\operatorname{ }300\]
| (%i25) | sr : 0 . 4244 ; sr_1 : 1 − sr ; |
\[\operatorname{ }0.4244\]
\[\operatorname{ }0.5756\]
| (%i28) | z_c : x2 · sr ; z_c_1 : x2 · sr_1 ; z_c + z_c_1 ; |
\[\operatorname{ }127.32\]
\[\operatorname{ }172.68\]
\[\operatorname{ }300.0\]
Created with wxMaxima.
The source of this Maxima session can be downloaded here.